Skip to main content

Section 7 Introduction to Fourier Series (a linear algebra perspective)

Subsection 7.1 Review of linear algebra

A vector space over a scalar field \(F\) is a collection of vectors together with operations that make it possible to do algebra on that collection. In particular, a set of vectors \(V\) is a vector space under the operations of addition and scalar multiplication if the following axioms are satisfied:

  1. associativity of addition: \(u, v, w \in V \Rightarrow u+(v+w) = (u+v)+w\)
  2. commutativity of addition: \(u, v \in V \Rightarrow u + v = v + u\)
  3. additive identity: there is an element \(0\text{,}\) the zero vector, so that \(v \in V \Rightarrow v + 0 = 0 + v = 0\)
  4. additive inverses: every vector \(v\) has an inverse \(-v\) \(\Rightarrow v + (-v) = 0\)
  5. compatibility: \(\alpha , \beta \in F, u \in V \Rightarrow (\alpha\beta)u = \alpha(\beta u)\)
  6. multiplicative identity: \(1 \in F, u \in V \Rightarrow 1u = u\)
  7. distribution over vector addition: \(\alpha \in F, u,v \in V \Rightarrow \alpha(u+v) = \alpha u + \alpha v\)
  8. distribution over field addition: \(\alpha, \beta \in F, u \in V \Rightarrow (\alpha + \beta) u = \alpha u + \beta u\)

The prototypical example of a vector space is \(n\)-dimensional Euclidean space, \(\R^n\text{,}\) our usual notion of vectors. However, many other sets of objects constitute vector spaces with the appropriate operations - for example, \(C([0,1])\text{,}\) the space of continuous functions on the interval \([0,1]\) is a vector space over \(\R\) under addition of functions. We are building to understanding spaces of functions.

Notice that the defintion of vector spaces doesn't include any way to multiply vectors. One notion of vector multiplication that you've likely seen before on \(\R^n\) is the dot product of vectors. Let \(v = (v_1, \ldots, v_n), u = (u_1, \ldots, u_n) \in \R^n\text{.}\) Then

\begin{equation*} u \cdot v = \sum_{i=1}^n v_i u_i. \end{equation*}

One of the most useful characteristics of the dot product on \(\R^n\) is that it allows a the definition of the angle between two vectors:

\begin{equation*} u \cdot v = \norm{u}\norm{v} \cos \theta \end{equation*}

where \(\theta\) is the angle between \(u\) and \(v\) and \(\norm{u} = \sqrt{u\cdot u}\text{.}\) Notice that when the vectors are perpendicular, this implies that the dot product is 0. We can generalize this geometry to the setting of general vector spaces.

The dot product is an example of a more general kind of product called an inner product on a vector space. Let \(V\) be a vector space over a field \(F\text{.}\) An operation \(\ip{}{}\) is called an inner product on \(V\) if

  1. positive definite: \(\ip{u}{u} > 0\) whenever \(u \neq 0\)
  2. conjugate symmetric: \(\ip{u}{v} = \cc{\ip{v}{u}}\)
  3. linear in the first entry: \(\ip{\alpha u + \beta v}{w} = \alpha \ip{u}{w} + \beta \ip{v}{w}\)

where \(\cc z\) denotes the complex conjugate. Note that in the case that the field \(F = \R\text{,}\) an inner product is symmetric.

A vector space \(V\) with an inner product that satisfies the axioms above is called an inner product space. One immediate feature of an inner product space is that the inner product defines a notion of length (or norm) of a vector:

\begin{equation*} \norm{v} = \sqrt{\ip{v}{v}}. \end{equation*}

The prototypical example is \(\R^n\) with the standard vector dot product. However, there are many others. For example, one extremely useful inner product space of functions is the vector space of functions \(f\) satisfying

\begin{equation*} \int \abs{f(x)}^2 \, dx \lt \infty \end{equation*}

- these are sometimes called functions of bounded energy and are referred to as the space \(L^2\) in mathematics. The inner product on \(L^2\) is given by

\begin{equation*} \ip{f}{g} = \int f(x)g(x) \, dx. \end{equation*}

In \(\R^n\text{,}\) two vectors are perpendicular when their dot product is 0 - that is, the angle between them is \(\pi/2\text{.}\) We will make the same definition more generally in inner product spaces, where we don't have a notion of angle, but we do have a notion related to the dot product - in an inner product space \(V\text{,}\) two vectors \(u\) and \(v\) are said to be orthogonal if \(\ip{u}{v} = 0\text{,}\) in which case we write \(u\perp v\text{.}\)

Every vector space \(V\) has a structural set of vectors called a basis, which can be used to build every other vector in the space - for example, the so-called standard basis of \(\R^3\) is the set \(\bbm 1\\0\\0 \ebm, \bbm 0\\1\\0 \ebm, \bbm 0\\0\\1\ebm\text{.}\) There are other bases for \(\R^3\text{,}\) in fact infinitely many.

Formally, a set of vectors \(\{b_i\}_I\) is a basis for \(V\) if

  1. linear independence: \(c_1 b_1 + \ldots + c_n b_n = 0\) has only the solution \(c_1 = c_2 = \ldots = c_n = 0\text{.}\)
  2. spanning set: every vector \(v \in V\) can be written as a linear combination of the \(b_i\text{.}\)

In fact, the linear combination of the \(b_i\) used to build \(v\) is unique when the \(b_i\) are a basis for \(V\) - in this case there exist unique constants \(c_1, \ldots, c_n\) so that

\begin{equation*} c_1 b_1 + \ldots + c_n b_n = v. \end{equation*}

The constants \(c_i\) are called the coordinates of v with respect to the basis \(\{b_i\}\text{.}\)

Now we'll blend orthogonality with basis and coordinates. If the vectors in a basis are pairwise orthogonal, then \(\{b_i\}\) is called an orthogonal basis. Furthermore, if the norm of each vector is 1, the basis is called orthonormal. It is exceptionally easy to compute coordinates of vectors when the basis is orthonormal.

This is standard in introductory linear algebra textbooks. I've elided a significant amount of geometric reasoning about projections here, to be filled in for completeness at some points.

The giant leap that we need to make is this - not every vector space is finite dimensional. An infinite dimensional inner product space is called a Hilbert space (whereas a finite dimensional inner product space is called a Euclidean space). For a Hilbert space, a basis will also be infinite dimensional. (If you're curious, the analogue of a matrix in the Hilbert space setting is called a linear operator, and the general study of these objects is called operator theory.) One of single most important ideas in engineering and modern science is that the set of \(L^2\) functions that are \(2\pi\)-periodic is a Hilbert space. In the next sections, we'll find a truly excellent orthonormal basis for that space of functions, and we'll begin to interpret the coefficients that we compute for a given function in terms of that basis. (This is the launching point of a field called signal analysis, typically found in electrical engineering.)

Subsection 7.2 The space \(L^2([-\pi,\pi])\)

(Note: the current draft of these notes is going to skip a lot of the theoretical development of \(L^2\) in favor of computing with it. As such, this draft should be considered a flavorful introduction rather than a rigorous treatment. Better a little taste than none at all.)

We're going to narrow our focus to one particular infinite dimensional Hilbert space. Consider the set of integrable functions \(f: [\pi,\pi] \to F\) that satisfy the condition

\begin{equation*} \int_{-\pi}^\pi \abs{f(x)}^2 \, dx \lt \infty. \end{equation*}

This set is a vector space under pointwise addition of functions and standard scalar multiplication. In addition, the product

\begin{equation*} \ip{f}{g} = \int_{-\pi}^\pi f(x)\cc{g(x)} \, dx \end{equation*}

is an inner product on \(V\text{.}\) The resulting inner product space (or Hilbert space) is called \(L^2([-\pi, \pi])\text{.}\) (We may shorten this to \(L^2\) in this section, with the understood restriction of domain.) The \(L^2\)-norm is given by

\begin{equation*} \norm{f}_{L^2} = \sqrt{\ip{f}{f}}. \end{equation*}

The following theorem, stated in this version in the spirit of Fourier, is one of the most important theorems in applied mathematics.

\(\cos nx\) and \(\sin nx\) are called harmonics, in analogy with the musical term.

The theorem is quite a bit more powerful than stated here. The proof requires some sophisticated machinery from the area of functional analysis, and will be sketched in sometime in the future. The main issue is one of convergence - why should an infinite series for an \(L^2\) function converge? What conditions need to be present on the coefficients of such a series to make this happen? For now, we suppress this discussion as outside the scope of the current objective, which is to treat the Fourier series as a black box and discover a method for computing the coefficients.

The form of the series in Theorem 7.2 is suggestive. If the \(\cos nx\) and \(\sin nx\) terms form an orthogonal basis for \(L^2\text{,}\) then we can use Theorem 7.1 to compute the mysterious coefficients \(a_n, b_n\text{.}\)

Leaving questions of convergence aside for the moment, let's check orthogonality. It should be clear that \(\ip{\sin(mx)}{\cos(nx)} = 0\text{.}\) (Hint: the integral of an odd function on a symmetric interval is 0). It remains to check that \(\sin mx \perp \sin nx\) and that \(\cos mx \perp \cos nx\) for \(m \neq n\text{.}\) The integrals are left as an exercise to the reader, with the hint that the appropriate starting place for the integrals is to use the identities

\begin{gather*} \cos(a)\cos(b) = \frac{1}{2} (\cos(a+b) + \cos(a - b))\\ \sin(a)\sin(b) = \frac{1}{2} (\cos(a-b) - \cos(a + b)) \end{gather*}

The double angle formulas can be used to establish that \(\norm{\cos nx}_{L^2} = \norm{\sin nx} = \sqrt{\pi}\text{,}\) and so we can create an orthonormal basis for \(L^2([-\pi,\pi])\) of the form

\begin{equation*} \{\frac{1}{\sqrt{2\pi}}, \frac{1}{\sqrt{\pi}}\cos x, \frac{1}{\sqrt{\pi}} \sin x, \frac{1}{\sqrt{\pi}} \cos 2x, \frac{1}{\sqrt{\pi}} \sin 2x, \ldots\}. \end{equation*}

Note 7.3.
You might wonder about this basis. After all, there are infinitely many different bases for \(\R^n\text{.}\) The same is true in \(L^2([-\pi,\pi]).\) The Fourier basis is chosen for work with periodic functions. There are other bases in the form of orthogonal polynomials of various flavors. Another basis is the complex exponential functions, which we can get from the Fourier basis using the identity \(e^{i\theta} = \cos \theta + i \sin \theta\text{.}\)

If we accept that convergence won't be an issue, we can now apply the Hilbert space analogue of Theorem 7.1: for \(f \in L^2([-\pi, \pi])\text{,}\) we have

\begin{align*} f \amp= \ip{f}{\frac{1}{\sqrt{2\pi}}} \frac{1}{\sqrt{2\pi}} + \ip{f}{\frac{1}{\sqrt{\pi}} \cos x}\cos x + \ip{f}{\frac{1}{\sqrt{\pi}}\sin x}\sin x + \ldots\\ \amp= \ip{f}{1} \frac{1}{2\pi} + \sum_{n=1}^\infty \frac{1}{\pi} \ip{f}{\cos nx} \cos nx + \frac{1}{\pi}\ip{f}{\sin nx} \sin nx. \end{align*}

We arrive at the computational formula for the Fourier coefficients \(a_n, b_n\) in Theorem 7.2.

\begin{align*} a_n \amp= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos nx \, dx\\ b_n \amp= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin nx \, dx \end{align*}

Subsection 7.3 Example computation

In this section, we'll build a Fourier series for a function that seems at first glance to be impossible to approximate with continuous period functions - the square wave. Square waves are not differentiable because they are full of jump discontinuities. Can we really hope to approximate such a function with sines and cosines?

We'll be using the function trapz(x,y) to compute numerical integrals from sample points. (In Octave, one can install the control and signal packages to have the function square already defined, but in this notes the function will have to be defined inline.) In the code example below, the accuracy of the approximation is set by the constant \(n\text{.}\) The default setting is \(n = 20\) (which is really only 10 terms, as the square wave we've defined is an odd function, and so the even harmonics integrate to zero).

The following code chunk, written in Sagemath, is an interactive illustration of the effect of increasing the number of terms.

Subsection 7.4 Complex numbers and Fourier series

Complex numbers are usually denoted in the form \(a + ib\) where \(i\) is the imaginary unit satisfying \(i^2 = -1\text{.}\) However, there is another useful form - if we think the complex numbers as giving \(x\) and \(y\) coordinates in the complex plane and \(a\) and \(b\) as the legs of a right triangle, then then hypoteneuse of the triangle will be \(r = \sqrt{a^2 + b^2}\text{,}\) and then angle at the origin will be \(\tan \theta = \frac{b}{a}\text{.}\) The quantity \(r\) is called the magnitude of a complex number and the angle \(\theta\) is called the argument.

Another important piece of working with complex numbers (a formula that physicist Richard Feynman called "the most remarkable theorem in mathematics") is Euler's formula, which allows the expression of movement around the unit circle in terms of a complex exponential function.

\begin{equation*} \cos \theta + i \sin \theta = e^{i \theta}. \end{equation*}

If you're interested in seeing why this might be true, consider the power series expansions for each of the functions in question to at least get a formal sense of the computation. (There isn't any prima facie reason to believe that complex numbers can just be plugged into infinite series, but it turns out to work very similarly to the real case.)

Combining Euler's formula with the right triangle picture of complex numbers gives the polar representation

\begin{equation*} z = r e^{i \theta}, \end{equation*}

where \(r\) is the radius or magnitude of \(z\) and \(e^{i \theta}\) is a point on the unit circle corresponding to the angle or argument \(\theta\text{.}\)

Fourier series can be reformulated into the complex exponential form using Euler's formula.

\begin{align*} \cos nx \amp= \frac{e^{inx} + e^{-inx}}{2}\\ \sin nx \amp= \frac{e^{inx} - e^{-inx}}{2i} \end{align*}

Then we can manipulate the trigonometric Fourier series as follows.

\begin{align*} f(x) \amp= \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos nx + b_n \sin nx\\ \amp= \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \frac{e^{inx} + e^{-inx}}{2} + b_n \frac{e^{inx} - e^{-inx}}{2i}\\ \amp= \frac{a_0}{2} + \sum_{n=1}^\infty \frac{a_n - ib_n}{2}e^{inx} + \frac{a_n + ib_n}{2} e^{-inx}\\ \amp= \sum_{\infty}^{\infty} c_n e^{inx} \end{align*}

where

\begin{align*} c_0 \amp= \frac{a_0}{2}\\ c_n \amp= \frac{a_n - ib_n}{2}\\ c_{-n} \amp= \frac{a_n + ib_n}{2}. \end{align*}

I want to stress the view that \(e^{ni\theta}\) corresponds to moving around the unit circle as \(\theta\) goes from \(-\pi\) to \(\pi\text{.}\) The larger \(n\) is, the faster the function travels around the circle, decreasing period and increasing frequency, just as in the cosine/sine case. To further push the analogy, we give the unit circle its own name, typically the fancy \(\T\text{.}\)

A little computation on \(a_n\) and \(b_n\) gives the following complex exponential form of Fourier series in \(L^2\text{.}\) (Alternatively, one can show that the set \(\{e^{\pm inx}\}_{n=1, \ldots, \infty}\) is an orthonormal basis for \(L^2\) and use the projection formula to generate the coordinate computation.)

Subsection 7.5 Introduction to the discrete Fourier transform

A sampled function results in a signal, that is a vector \(x = [x_0, \ldots, x_{n}]\text{.}\) This is a discrete object. We used integral approximations to estimate the Fourier coefficients of such an object in the previous sections by assuming that the signal represented a continuous function \(f(t)\text{.}\) However, given that signals are discrete, it seems useful to introduce a discrete method for recovering Fourier coefficients.

The method that we (very very briefly) introduce here is called the discrete Fourier transform. A signal \(x = (x_n)_{n=0, \ldots, N-1}\) lives in the time domain - that is, we think of the array indicies as corresponding to an independent variable in time. The entries of the array represent the magnitude of the signal at time \(k\text{.}\) The discrete Fourier series will produce a vector of the same length, but in the frequency domain - that is, the array indicies will correspond to frequencies. The entries of the array will be complex numbers representing the amplitude and phase shift of the corresponding frequency \(k\text{.}\) The discrete Fourier transform takes a signal in the time domain and produces an array (really a function) in the frequency domain.

Definition 7.5.
Let \(x = (x_n)_{n = 0, \ldots, N-1}\) be a signal in the time domain. Then the DFT of \(x\) is the vector \(X\) with complex entries given by
\begin{equation*} X_k = \frac{1}{N} \sum_{n=0}^{N - 1} x_n e^{-i2\pi \frac{k}{N}n}. \end{equation*}

Before we talk about how the DFT works, we can talk about what it produces. First, frequencies in this setting are with respect to \(N\text{,}\) the length of the signal. A frequency of \(k\) corresponds to a pattern that is repeated \(k\) times over \(N\) terms. In other words, the period of the pattern is \(\frac{N}{k}\text{.}\) Each \(X_k\) is a complex number that contains the amplitude and phase shift of the corresponding harmonic that describes the pattern. That is, if a harmonic of frequency \(k\) is hidden in a signal, the magnitude \(\abs{X_k}\) will be significantly larger than the magnitude of the “noise” present. Plotting the frequencies reveals which harmonics are present.

We can illustrate how the DFT works with an example composite signal. Let \(v_1 = [1, -1, 1, -1, 1, -1, 1, -1, 1, -1, 1, -1]\) and \(v_2 = [3, -4, -1, 3, -4, -1, 3, -4, -1, 3, -4, -1]\text{.}\) Relative to the length of the signal, \(v_1\) has frequency 6 and \(v_2\) has frequency 4. If we add the signals, we get the composite vector

\begin{equation*} v_1 + v_2 = x = [4, -5, 0, 2, -3, -2, 4, -5, 0, 2, -3, -2 ], \end{equation*}

which looks to have frequency 2. The DFT should recover that the signal \(x\) has harmonics at frequencies 6 and 4. The computation essentially converts the problem into a vector addition problem. We can illustrate by looking at the graphs corresponding to the computation of \(X_1\) and \(X_4\text{.}\) We should expect \(\abs{X_1} = 0\) and \(\abs{X_4} >> 0\text{,}\) as a component signal of frequency 1 is not present and a signal of frequence 4 is.

\begin{equation*} X_1 = \frac{1}{12}\left(4 -5 e^{-i2\pi\frac{1}{12}} + 0 e^{-i2\pi\frac{2}{12}} + \ldots -2 e^{-i2\pi\frac{11}{12}}\right) \end{equation*}

Essentially, this is a vector addition problem, as the following figure should make clear.

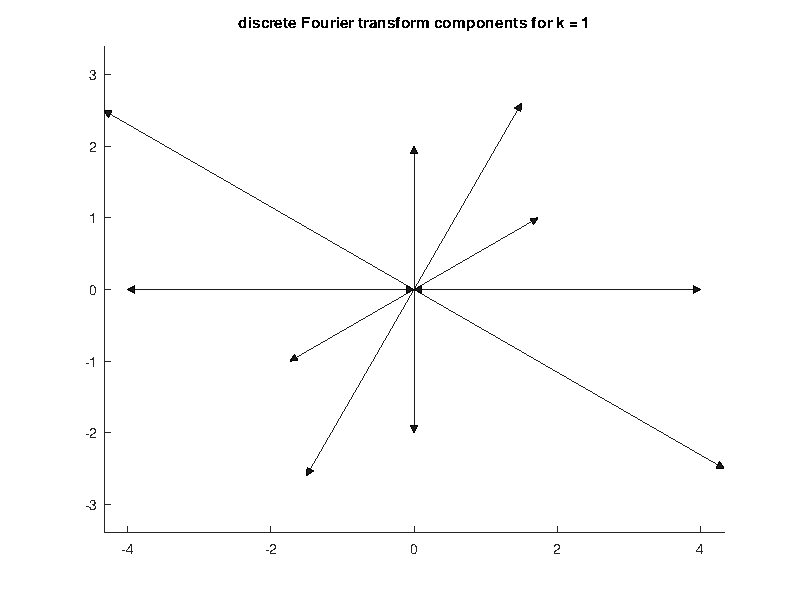
Visually, it should be apparent that the sum of these vectors is 0.

On the other hand, we can look at a frequency that is present in \(x\text{,}\) say \(X_4\text{.}\) We compute

\begin{equation*} X_4 = \frac{1}{12}\left(4 -5 e^{-i2\pi\frac{4}{12}} + 0 e^{-i2\pi\frac{8}{12}} + \ldots -2 e^{-i2\pi\frac{44}{12}}\right) \end{equation*}

which is an addition of this set of vectors, clearly a set with a non-zero sum.

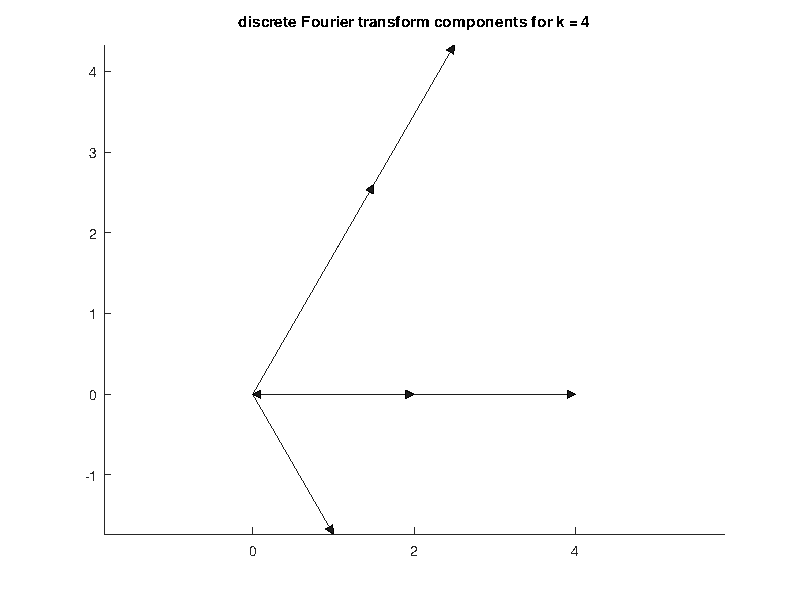
That this vector has non-zero magnitude should not be surprising, given that a pattern of frequency 4 is one of the constituent signals in \(x\text{.}\)

Subsection 7.6 Leakage and the DFT

To be added.

Subsection 7.7 Octave and the DFT

Of course in practice, signals are thousands or millions of entries long. We don't want to have to compute millions of entries for the frequency domain function by hand. Instead, we use an implementation of the DFT called the fast Fourier transform, an algorithm that is outside the scope of these notes. What you need to know about the command fft is that it produces most of \(X\) for a signal \(x\) in the time domain. The part that it leaves out is the normalization \(1/N\) that accounts for the total energy contained in a signal (longer signals mean more energy).

\begin{equation*} \mathrm{fft}(x) = \left[\sum_{n=0}^{N-1} x_k e^{-i2\pi\frac{k}{N}n}\right]_{k=0, \ldots, N-1}. \end{equation*}

That is, the entries of fft(x) are the unnormalized discrete Fourier coefficients \(N X_k\text{.}\)

Let's take a look at our signal from the previous section.

Several things should be immediately apparent. The first is that (with the exception of the term at \(k=0\text{,}\) which is special) the plot is symmetric about the line \(k = 6\text{.}\) The reason is that once you go beyond the midpoint of the vector, you are recovering the harmonic corresponding to the backwards frequency \(k\text{,}\) which will have the same magnitude as the forwards frequency \(k\) for real signals. This will be apparent if you look at how the points move around the unit circle. (For example, compare how multiples of \(\frac{\pi}{6}\) and \(\frac{11 \pi}{6}\) traverse the circle.) Thus, the frequency \(k\) for a real signal has two components of equal magnitude that contribute to that harmonic (much like the sine and cosine contribute to a single harmonic in the trigonometric setting). The special nodes are at \(k = 0 \text{,}\) which electrical engineers call the DC component (that is, the center of oscilliation for the signal), and at \(k = N/2\) which is called the Nyquist frequency, beyond which no frequency can be detected.

Since we want all of the frequencies between the DC component and the Nyquist frequency to count twice, we'll construct the following one-sided spectrum.

This shows precisely what we expect - the 0 frequency reflects the fact that the signal isn't centered about the x-axis. The \(k=4\) and \(k=6\) values reflect the constituent patterns from \(v_1\) and \(v_2\text{.}\)

One of the extremely useful features of the DFT is how good it is at pulling signal out of noise. Consider the following example. We're going to construct a signal with units inherited from a known sample rate. Suppose we have a signal that we sample at a rate of \(Fs\) Hz. Then each increase in array position corresponds to a time step of \(\Delta t = 1/Fs\) seconds. Given a signal of length \(L\text{,}\) the total time of the signal will be \(T = L\times\Delta t\text{.}\) Knowing the sample rate will allow us to explicitly interpret the spectral analysis in terms of the input signal frequencies. (That is, we'll be able to attach units to our spectrum.)

The following example constructs a nice period function from a sum of sines and cosines, then corrupts the signal with random noies. The fft can be used to produce a one-sided spectrum that recovers the frequences of the original signal.

Subsection 7.8 Going backwards - ifft

We've seen that fft takes a signal \(x\) in the time domain and produces a vector \(X\) in the frequency domain. Since each entry in \(X\) is a linear combination of the entries of \(x\text{,}\) we should suspect that this process can be inverted. Indeed, inverse DFT , implemented in Octave as ifft, takes a frequency vector \(X\) and produces a time domain signal \(x\text{.}\) Note that since we normalized the output of fft by dividing by the length of the vector (since fft(x)\(= \sum_{n=0}^{N-1} x_k e^{i2\pi \frac{k}{N} n}\)), we need to undo the normalization before we compute the ifft.

login